サムネイルがまんま結論の一部です&タイトルでビビッと来たアナタ（+野球好き）が対象読者です.

ちょっとやりたいことがあって,

やりたいこと⚾のサンプルがたまたまRだった
このあと自分で分析したりなにか作るんやったらPythonでやりたい
せや！RからPythonに移植しちゃえば良いンゴ

ってことで, 粛々とRからPythonに移植した時に気がついた事をサラッと書きたいと思います.

最初に断っておくと,

RよりPythonが優秀（またはその逆）だから書き換える！って意味ではありません！

どっちが優秀だの, 好みは何だのといった所は（必要と思った箇所を除き）触れないのでご了承ください.*1

というわけで, 変に力んだりマウントを取ること無く, ごゆるりとおくつろぎながら読んでもらえると幸いです.

TL;DR

数式を意識しながら読んだり, 統計的にいい感じにしたい時はRの方がしっくりくる.
一方, プログラミングな解釈および, プログラマーな指向性（嗜好性）でやるならPython.
我思う, どっちを選ぶかは何をやりたいか・もしくは個人の好みなんじゃないかと.
PythonとR（でも他の言語でも）を行き来するならJupyter notebook便利やぞ

本日のスタメン

TL;DR
本日のスタメン
やりたいこと
- 野球の統計分析
RとPythonの違いをコードから読み解く
結び - RとPythonどっち使う問題
- RとPythonとSQLの違い
- 自分は結局どちらを使うのか！？
[補足]参考書籍・参考サイト
- 書籍
- Webサイト

やりたいこと

先にやりたいこと（要件）を軽く.

野球の統計分析

（プロとしての仕事じゃなくなりましたが）とあるテーマを元に趣味で⚾の分析やってます.

そんな中で, このブログでも何回か登場しているこちらの書籍*2.

Analyzing Baseball Data with R, Second Edition (Chapman & Hall/CRC The R Series)

作者: Max Marchi,Jim Albert,Benjamin S. Baumer
出版社/メーカー: Chapman and Hall/CRC
発売日: 2018/12/04
メディア: ペーパーバック
この商品を含むブログを見る

名前の通り, 「野球のデータ分析しちゃおうぜー, Rで」っていう本なのですが, この中に登場する,

Career Trajectories（年数に伴う成績の軌跡*3）
Simulation（読んで字の如しなアレ*4）

これをRで学びながら, 理解（と今後やりたいこと）に合わせて,

本の通りRで写経
Rのコードをいい感じに解釈しながらPythonに移植しよ

ということをやろうと思い, ここ数週間お試ししてました.

このエントリーで扱う内容はそんな写経で得たなにかです.

なお, 読み進めるに当たり, 特段野球の知識はいらないと思います.

RとPythonの違いをコードから読み解く

というわけで, 実際やってみましたので, コードも交えてちょいと解説します.

事前準備（環境構築）

何をやるにも環境作りからですよねと.

具体的には,

Python 3系が動く環境
かつ, Jupyter notebookの設定が出来ていて
JupyterからRが使える（IRKernelが入ってる）

ことが条件となります.

Python + Jupyter

拙作で恐縮ですが, こちらのエントリーと同じ環境を揃えてもらえればOKです.

shinyorke.hatenablog.com

いやいや, 私はAnacondaの方が好みだよ！って方は, いい感じに読み替えるか, この辺を見るか, このあと紹介するRの環境設定が乗っているこちらをご覧ください.

PythonユーザのためのJupyter[実践]入門

作者: 池内孝啓,片柳薫子,岩尾エマはるか,@driller
出版社/メーカー: 技術評論社
発売日: 2017/09/09
メディア: 大型本
この商品を含むブログ (1件) を見る

また, condaもしくはpipでこちらのライブラリも入れましょう（いずれも最新版で）.

numpy
scipy
pandas
scikit-learn
bokeh

さらに追加でこちらをpipで入れましょう（これはcondaに対応していない）

sabr ※野球統計（セイバーメトリクス）のライブラリ*5です（shinyorke作）.

$ jupyter notebook

上記コマンドでnotebookが立ち上がり, 上記コマンドが使えるようになっていればOKです.

R

Rを使いたい時は, 統合開発環境（という言い回しで合ってるはず）のR Studioを入れるのが常套手段ですが今回は,

RとPythonを行き来する
同じ画面・同じ機能でお互い行き来出来たほうが生産性も良さげ

って事で,

IRkernelを入れる
Jupyter notebook作成時にRを指定して読み書きする

方法で行います*6.

Rをインストールする

CRANプロジェクトで紹介されてる方法もしくは, Mac OSの方はbrewでインストール.

ここは特につまりどころは無いと思うのでサクサクいけるかなと.

IRkernelをインストールする

昔はCRAN（Rのライブラリのリポジトリ, Pythonで言うところのPyPI）に無かったらしいのですが, 今はCRANにあるのでRを立ち上げて,

> install.packages('IRkernel')

これでインストールできます.

動作確認ですが, Jupyter notebookもしくはJupyter labでKernelが認識され, Hello Worldできるくらいまで確認できれば問題ないかと.

f:id:shinyorke:20191117150801p:plain — Jupyter notebookの場合

f:id:shinyorke:20191117150823p:plain — Jupyter Labだと

分析パッケージのインストール

同じくRのインストールコマンドで,

tidyverse（統計パッケージ）
Lahman（メジャーリーグのデータセット）

を入れます.

> install.packages('tidyverse')
> install.packages('Lahman')

ここまでできるとこのあとのスニペットを元に真似ができる（はず）です.

題材「とある大打者のOPS推移と近似する成長曲線を描く」

大昔にプレーしていたニューヨーク・ヤンキースの大打者, ミッキー・マントルのOPS（出塁率 + 長打率）の推移を年齢ごとに見つつ, それに近似する成長曲線を書こうというのがテーマとなります.*7

書籍における, オリジナルのコードはこちらになります.

見比べると面白いと思います.

コードを比較

Rのコード（オリジナルを一部変更して写経）

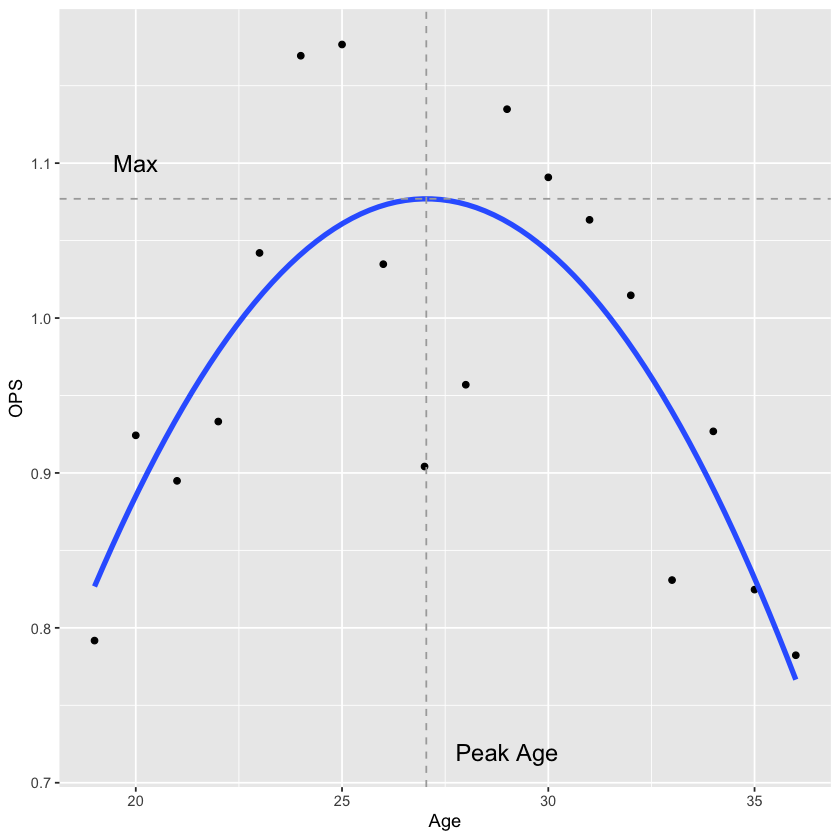
ミッキー・マントル(MLB)のOPS推移とパフォーマンス軌跡

出来上がりのグラフはこちらです.

f:id:shinyorke:20191117152628p:plain — R版（本と同じ）

Pythonのコード

ミッキー・マントル(MLB)のOPS推移とパフォーマンス軌跡 - Python版

Python版だとグラフはこんな感じです（似せる努力はそこそこした）.

f:id:shinyorke:20191117152722p:plain — Python（bokeh）版

曲線は若干カクカクしてますが, これは内部的にHTML Canvasを使って描画している（BokehそのものがD3.jsベースなので）であり,

matplotlibなど, ラスターでちゃんと書くとほぼ同じ見た目になるはずです.*8

完成したグラフを比較

Pythonの曲線がカクカクしてる以外は大差なさそうです.

f:id:shinyorke:20191117171653p:plain — どちらもそんなに変わりませんね

なかなかいい感じでしたってことで.

違いを確かめる

ここで, 同じような処理をしているところをRとPythonで比較してみます.

データの取得と加工

CSVからミッキー・マントルのデータを取り出し, OPSなどを計算している箇所を比較します.

Rの場合

Masterデータから選手データを取得, Battingの全量データを取得中に指標を計算.

Master %>%
  filter(nameFirst == "Mickey", nameLast == "Mantle") %>%
  pull(playerID) -> mantle_id

batting <- Batting %>%
  replace_na(list(SF = 0, HBP = 0))

get_stats <- function(player.id) {
    batting %>%
      filter(playerID == player.id) %>%
      inner_join(Master, by = "playerID") %>%
      mutate(birthyear = ifelse(birthMonth >= 7, birthYear + 1, birthYear),
                    Age = yearID - birthyear,
                    SLG = (H - X2B - X3B - HR +  2 * X2B + 3 * X3B + 4 * HR) / AB,
                    OBP = (H + BB + HBP) / (AB + BB + HBP +SF),
                    OPS = SLG + OBP) %>%
     select(Age, SLG, OBP, OPS)
}

Mantle <- get_stats(mantle_id)

Pythonの場合

R版と同じデータを全量読み込んだあと, pandasで愚直に前処理しています.

年齢・指標計算は関数として切り出し, applyでつなぎこみ.

import csv
import pandas as pd
pd.options.display.max_columns = 100

players = {}
with open("/Users/hoge/github/baseballdatabank/core/People.csv", "r") as f:
    reader = csv.DictReader(f)
    players = {r['playerID'] : r  for r in reader}

df_batting = pd.read_csv("/Users/hoge/github/baseballdatabank/core/Batting.csv")
df_batting.fillna(0.0, inplace=True)

def player_name(playerID: str) -> str :
    if playerID in players:
        return str(f"{players[playerID]['nameFirst']} {players[playerID]['nameLast']}")
    return 'Unknown'

def age(row: pd.Series) -> int :
    if row.playerID in players:
        player = players[row.playerID]
        birthYear = player['birthYear']
        if birthYear:
            birthYear = int(birthYear)
        else:
            return None
        return row.yearID - birthYear - 1
    return None

df_batting['playerName'] = df_batting['playerID'].map(player_name)
df_batting['age'] = df_batting.apply(age, axis=1)
df_batting['SINGLE'] = df_batting['H'] - (df_batting['HR'] +  df_batting['3B'] +  df_batting['2B'])
df_batting['TB'] = df_batting['HR'] * 4 + df_batting['3B'] * 3 + df_batting['2B'] * 2 + df_batting['SINGLE'] * 1

# 打率, 出塁率, 長打率. 指標値計算にSABRを使う

import sabr

from sabr.stats import Stats
def ba(row: pd.Series) -> float:
    try:
        return Stats.avg(ab=row.AB, h=row.H)
    except ZeroDivisionError as e:
        return 0.0

def obp(row: pd.Series) -> float:
    try:
        return Stats.obp(ab=row.AB, h=row.H, bb=row.BB, sf=row.SF, hbp=row.HBP)
    except ZeroDivisionError as e:
        return 0.0

def slg(row: pd.Series) -> float:
    try:
        return Stats.slg(ab=row.AB, tb=row.TB)
    except ZeroDivisionError as e:
        return 0.0

df_batting['BA'] = df_batting.apply(ba, axis=1)
df_batting['OBP'] = df_batting.apply(obp, axis=1)
df_batting['SLG'] = df_batting.apply(slg, axis=1)
df_batting['OPS'] = df_batting['OBP'] + df_batting['SLG']

df_mantle = df_batting.query("playerName == 'Mickey Mantle'")

df_mantle[['age', 'SLG', 'OBP', 'OPS']]

Rの方がスッキリ, Pythonはプログラミングっぽい

データがCSVで比較的正規化されているせいか, Rの方は記述量が圧倒的に少ない印象を受けました.

一方Pythonはまだコードを減らせる余地ある（中身を確認しながらやってるため敢えて冗長になってます）とはいえ, 記述量が多くて長い.

線形回帰の計算

Rは標準の関数かな？よくわかってませんこの辺.

Pythonはお馴染みscikit-learnをそのまま使います.

なお, 線形回帰のモデルは,

目的変数はOPS
説明変数は年齢をアレンジしたもの

となっております（中身気になる人は書籍の方を読んでね, ここでは説明しません）.

Rの場合

線形回帰モデルを関数で作り込んだあと, Mantleデータを流し込み.

fit_model <- function(d) {
    fit <- lm(OPS ~ I(Age - 30) + I((Age - 30) ^2), data = d)
    b <- coef(fit)
    Age.max <- 30 -b[2] / b[3] / 2
    Max <- b[1] - b[2] ^ 2 / b[3] / 4
    Max2 <- b
    list(fit = fit, Age.max = Age.max, Max = Max)
}

F2 <- fit_model(Mantle)

coef(F2$fit)

c(F2$Age.max, F2$Max)

Pythonの場合

目的変数, 説明変数を作り込んだ上でsciket-learnへ.

from sklearn.linear_model import LinearRegression

Y = df_mantle['OPS'].values

_df_x = pd.DataFrame()
_df_x['I(Age-30)'] = df_mantle['age'] - 30
_df_x['I((Age-30)^2)'] =  (df_mantle['age'] - 30) ** 2
X = _df_x[['I(Age-30)', 'I((Age-30)^2)']].values

ml = LinearRegression()
ml.fit(X, Y)

age_max = 30 - (ml.coef_[0] / ml.coef_[1] / 2)
_max = ml.intercept_ - ml.coef_[0] ** 2 / ml.coef_[1] / 4
age_max, _max

数式を意識するならR, 記述の順番・容易性はPython?

自分がプログラマー上がりでPythonなアプローチに慣れていること, 数学よりの人間じゃないことよりそんな印象を受けました.

数式・モデルを説明するならRの方がやはりスッキリしてる感あります.

一方, Pythonは,

インスタンス作って
目的変数・説明変数の行列作って
fitしてあとはよしなに

っていう定番の流れはコード書く時にすごくやりやすいなって印象あります.*9

これはまあ目的と好みによってどっち使う的なのあっていいかなって思います

グラフ描画

最後の描画部分です.

Rの場合

お決まりのggplotで.

ggplot(Mantle, aes(Age, OPS)) + geom_point() +
  geom_smooth(method = "lm", se = FALSE, size = 1.5, formula = y ~ poly(x, 2, raw = TRUE)) +
  geom_vline(xintercept = F2$Age.max, linetype = "dashed", color = "darkgrey") +
  geom_hline(yintercept = F2$Max, linetype = "dashed", color = "darkgrey") +
  annotate(geom = "text", x = c(29, 20), y = c(0.72, 1.1), label = c("Peak Age", "Max"), size = 5)

Pythonの場合

こちらはbokehで.

matplotlibなど, 他を使うと印象変わるのであくまで参考程度.

# OPS + Peak Ageを可視化
from scipy.interpolate import CubicSpline
import numpy as np
from bokeh.models import Span, ColumnDataSource, LabelSet

output_notebook()

# Vertical line
vline = Span(location=age_max, dimension='height', line_color='black', line_dash='dashed', line_width=1)
# Horizontal line
hline = Span(location=_max, dimension='width', line_color='black', line_dash='dashed', line_width=1)

x = df_mantle['age'].values
y=  df_mantle['OPS'].values


res = np.polyfit(x,  y, 2)
y1 = np.poly1d(res)(x)
spl = CubicSpline(x, y1)
y_smooth = spl(x)

# Label
source = ColumnDataSource(data=dict(ops=[y[0], _max], 
                                    age=[age_max, x[0]],
                                    names=['Peak Age', 'Max']))
labels = LabelSet(x='age', y='ops', text='names', level='glyph', x_offset=5, y_offset=5, source=source, render_mode='canvas')



p = figure(
    plot_width=840, 
    plot_height=840, 
    title="Mickey Mantle OPS",
    x_axis_label='AGE',
    y_axis_label='OPS',
)
p.circle(x='age', y='OPS', size=4, source=df_mantle, fill_color='black', line_color='black')
p.line(x, y_smooth, line_color='blue')
p.add_layout(vline)
p.add_layout(hline)
p.add_layout(labels)

show(p)

記述量の差はあれど, どちらも方言だよね説.

まず個人的に思ったのが, ggplot優秀すぎるやろ！

bokehで書いた方は昨日に半日かけて仕上げたのですが色々めんどくさかったです, 使い慣れてるはずなのに.

ただ, これも好みというか方言の違い程度かなって思っていて,

数式を意識しながら試し打ちするならやっぱRだしggplotはそのための道具
分析したモデルをそのまま流用（例えばシステムとかアプリに）って意味ではPythonの方が強い.描画もそっちの指向がちょっと入ってる

という認識のもとでいるとまあこの違いも当然だよな感あります.

結び - RとPythonどっち使う問題

今回は野球の統計分析をテーマに見てきましたが,

？？？「そもそもRとPythonどっち使えば良いンゴ？」

についてまとめつつ終わりたいなと.

RとPythonとSQLの違い

本格的に結ぶ前に,

前処理大全[データ分析のためのSQL/R/Python実践テクニック]

作者: 本橋智光
出版社/メーカー: 技術評論社
発売日: 2018/04/13
メディア: 大型本
この商品を含むブログ (1件) を見る

こちらを参考に自分なりの考えを踏まえた上で, RとPython, そしてデータ取得・加工といえばSQLってことでこの三者の比較しました.

比較項目	R	Python	SQL（データベース）
記述量	少ない	普通	多い
処理速度	やや遅い	速い（というかチューニング効く*10）	速い
*分散処理11**	頑張ればできる	頑張ればできる	できる（というかそれが普通）
分析以外での運用（アプリなど）	普通はやらない（出来なくはない）	得意中の得意	もちろんできる
計算処理	数式モデルな感じが得意	プログラミング的な解釈だと最高に良い	できるけど, 神functionみたいな地獄が(ry
可視化・描画	分析・解析目当てなら十分すぎる	色んな方法で可視化できる, Webアプリ含めて	無い. 普通はやらない.